Pusing dengan matematika? Pelajaran yang satu ini memang sering membuatmu ingin menutup buku saja. Namun, tetap saja ini salah satu ilmu yang berguna dihidupmu. Trik untuk bisa menyelesaikan soal matematika adalah dengan memahami rumus dasar dan rajin mengerjakan berbagai macam tipe soal. Yuk lihat soal kelas 11 SMA matematika dibawah ini sebagai referensi belajarmu.
1. Area parkir adalah 1.760 m2. Luas nya untuk 4 m2 mobil dan 20 m2 mobil. Kapasitas sebagai hanya 200 kendaraan dengan biaya adalah 1.000 IDR / jam sebagai mobil kecil dan 2.000 IDR / jam sebagai mobil besar. Jika terisi penuh maka kendaraan yang melaju akan datang, hasil akhir adalah...
A. Rp.176.000
B. Rp.200.000
C. Rp.260.000
D. Rp.300.000
E. Rp.340.000
2. Perkalian x4 – 3×2 + kapak + b jika dibagi dengan x2 – 3x – 4 sisanya adalah 2x + 5, maka nilai a dan b...
A. A = -35, b = 40
B. A = -35, b = -40
C. A = 35, b = 40
D. A = 40, b = -35
E. A = -40, b = -35
3. Perusahaan perumahan berencana membangun rumah tipe A dan B. Setiap unit apartemen A membutuhkan petak 150 m2 dan rumah tipe B seluas 200 m2. Tanah yang tersedia adalah 30.000 m2. Perusahaan dapat membangun maksimal 180 unit.
Keuntungan yang diharapkan untuk setiap unit rumah tipe A adalah IDR 3.000.000,00 dan IDR 4.000.000 untuk tipe B. Rumah-rumah individu berikut harus dibangun untuk keuntungan maksimum:
A. 140 unit tipe A dan 40 unit tipe B
B. 120 unit tipe A dan 60 unit tipe B
C. 100 unit tipe A dan 80 unit tipe B
D. Hanya 180 unit tipe A
E. Hanya 150 unit tipe B
4. Suku banyak 2𝑥5 − 3𝑥4 − 𝑥2 + 2𝑥 − 1 dibagi 𝑥3 − 1, maka sisanya adalah...
A. 𝑥2 − 𝑥 − 1
B. 𝑥2 − 𝑥
C. −3𝑥2 − 𝑥 + 1
D. 𝑥2 + 𝑥 − 1
E. 𝑥2 + 2𝑥 − 1
5. Jika 𝑓(𝑥) = 2𝑥² + 5𝑥 dan 𝑔(𝑥) = 1/𝑥 maka (f o g)(2) adalah…
A. 3
B. 2
C. 1
D. ½
E. 1/3
6. Ada 40 jam untuk mencair, 20 jam untuk roll dan 60 jam untuk memotong. Jika x adalah banyak baja tipe I dan y adalah banyak baja tipe II dan x ≥ 0 dan y ≥ 0, model matematika lainnya adalah:
A. 2x + 5y ≤ 40, 4x + y ≤ 20, 10x + 5y ≤ 60
B. 2x + 5thn ≤ 40, 4x + y ≥ 20, 10x + 5thn ≤ 60
C. 2x + 5y ≤ 40, 4x + y ≤ 20, 10x + 5y ≥ 60
D. 2x + 5y ≥ 40, 4x + y ≤ 20, 10x + 5y ≥ 60
E. 2x + 5y ≥ 40, 4x + y ≥ 20, 10x + 5y ≥ 60
7. Persamaan garis sejajar dengan garis 2x + y = 2 = 0 dan melalui titik (−2.3) adalah:
A. 2x + y + 1 = 0 d. 2x – y – 1 = 0
B. 2x + y – 1 = 0 e. −2x + y + 1 = 0
C. 2x – y + 1 = 0
D. −2x + y + 1 = 0
E. 2x – y – 1 = 0
8. Jika fungsi g (x) = 2x + 1 dan (kabut) (x) = 8×2 + 2x + 11 diberikan, rumus f (x)...
A. 2×2 + 3x + 12
B. 2×2 – 3x – 12
C. 3 × 2 – 2 × + 12
D. 2×2 – 3x + 12
E. 3×2 + 2x -12
9. Fungsi f (x) dibagi x – 1 adalah 3, sedangkan bila dibagi x – 2 sisanya adalah 4. Jika f (x) dibagi x2 – 3x + 2, maka sisanya...
A. 2x + 2
B. -x – 2
C. X + 2
D. X - 2
E. -x + 2
10. Sebuah kotak berisi 5 bola merah, 4 biru dan 3 kuning. 3 bola dihapus secara acak dari kotak sekaligus. Probabilitas bahwa 2 bola merah dan 1 biru adalah...
A. 1/10
B. 5/36
C. 1/6
D. 2/11
E. 4/11
11. Tiga puluh orang siswa di kelas A memperoleh rata-rata nilai ulangan matematika 78. Sedangkan di kelas B yang jumlah siswanya 10 orang lebih sedikit dari kelas A mempunyai rata-rata 83. Apabila kedua kelas tersebut digabungkan, maka rata-rata gabungan kedua kelas tersebut adalah...
A. 75
B. 79
C. 80
D. 82
E. 83
12. Tiga siswa dan tiga siswi duduk berjajar pada sebuah bangku. Jika yang menempati pinggir bangku harus siswa, banyaknya susunan posisi duduk yang mungkin adalah...
A. 6
B. 24
C. 120
D. 144
E. 720
13. Pada pengambilan sebuah kartu secara acak pada seperangkat kartu bridge. Peluang terambilnya kartu merah bergambar orang adalah ….
A. 3/13
B. 3/26
C. 4/13
D. 5/26
E. 12/13
14. Nilai rata-rata tes suatu lomba matematika dari 20 orang siswa adalah 25. Jika nilai rata-rata 8 orang siswa dari 20 siswa tersebut adalah 10, maka nilai rata-rata dari 12 siswa lainnya adalah...
A. 25
B. 28
C. 30
D. 35
E. 40
15. Pusat dan jari-jari lingkaran yang persamaannya x2 + y2 – 8x + 4y – 5 = 0 berturut-turut adalah...
A. (2, 3) dan 5
B. (2, 8) dan 10
C. (4, -2) dan 5
D. (8, 4) dan 10
E. (-2,8) dan 5
16. Jika titik (-5,k) terletak pada lingkaran x2 + y2 + 2x – 5y – 21= 0 maka nilai k adalah...
A. -1 atau 2
B. 1 atau -2
C. -1 atau 6
D. 1 atau -6
E. 2 atau -6
17. Persamaan lingkaran yang berdiameter ruas garis AB dimana titik A(-3,2) dan B(3,-2) adalah...
A x2 + y2 = 26
B x2 + y2 = 13
C x2 + y2 = 4
D x2 + y2 = 52
E x2 + y2 = 36
18. Jika
A. 3
B. 2/3
C. -2
D. 1/3
E. ¾
19. Invers dari fungsi 𝑓(𝑥) = 5𝑥−1− 3 adalah...
a. log5 (5𝑥 + 15)
b. log5 (𝑥 + 4)
c. log5 (𝑥 + 3)
d. -1 + log5 (𝑥 + 3)
e. 1 − log5 (𝑥 + 3)
20. Diketahui 𝑓(𝑥) = 1/𝑥 dan 𝑔(𝑥) = 2𝑥 −1 maka nilai (𝑔‾¹𝑜𝑓‾¹)(𝑥) adalah...
Jawaban : B
Apakah sudah cukup banyak coretanmu untuk menghitung rumus-rumus tersebut? Jika belum, ayo terus mencoba menyelesaikannya. Jangan ragu untuk membuka catatanmu. Mengerjakan soal matematika itu menyenangkan jika kamu sudah terbiasa, tentunya juga dibantu pemahaman rumus dasar. Selain itu, pelajaran hitung-menghitung ini akan membuatmu lebih fokus dalam belajar.



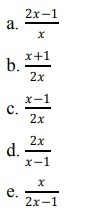
Post a Comment